Ulam–Warburton automaton inquiry

The Ulam-Warburton automaton is a simple growing pattern. See Wikipedia or this great Numberphile video for more information. For the more technical see this paper too.

Ulam-Warburton animation from Wikipedia

I was curious what you'd get under various other versions of it, using the same basic rule of "turn on cells with exactly one neighbor" but with a tweak. For example, what happens if you a cell turns off after being activated for a few cycles?

You get this beautiful modification. I plan to follow this up more and will make code available then (although it's insanely simple). I would be curious what statements you can make about the periodicity and the number of active cells at any time.

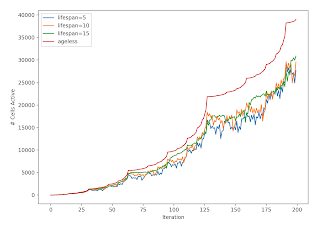
For example, empirically it seems that the number of cells in a "dying" version is always upper bounded by the ageless and standard Ulam-Warburton Automaton. Now, prove that and derive formulas (or prove it's not possible) for a generalized version.

Other ideas:

• How does the total cell count formula change depending on the starting configuration, e.g. more than one active cell?
• Are there interesting stochastic versions?
• What happens when cells have a regeneration period, a time after they die before they can activate again? That models disease and other phenomena better maybe since resources/population has to restore before a new outbreak is successful.
• What if the age of a cell is a function of its position on the plane?
• Can we generalize to other grid types?
• How does this fit into other work? Has it already been done?

This whole curiosity partially started because I wanted to assign a simple proof about Ulam-Warburton to my summer discrete math class. I also have an affinity for fractals, who doesn't?